Deriving HRC-I Degap for XRCF Settings

Linear Degap Coefficients

Linear coefficients will shift all events away from the coarse position by a constant fraction. These can be selected by generating projections for a series of linear degap coefficients and then selecting for each gap the coefficient that removes the gap. The figure below shows the result of doing this for the HRC-I "XRCF" flat-field data set. The degap coefficients are given here. While the coefficients vary from tap to tap, the average coefficient for the U-axis is 1.054 and for the V-axis it is 1.037.

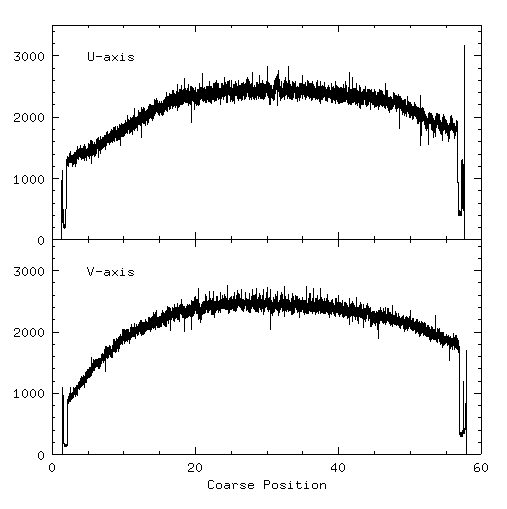
Projections: HRC-I Linear Degapped Flat-Fields at XRCF Settings

The resulting histograms show little evidence for residual gaps. This set of coefficients have been used by the ASCDS for all reprocessing of HRC-I XRCF data since August 1997. Expanded views of a few sections of the histograms, comparing the raw (undegapped) to the linear degapped data, are shown below (click on image to get full view).

Projections: HRC-I Raw and Linear Degapped U-axis Coarse Positions 25-35 Projections: HRC-I Raw and Linear Degapped V-axis Coarse Positions 25-35 Projections: HRC-I Raw and Linear Degapped U-axis Coarse Positions 50-60 Projections: HRC-I Raw and Linear Degapped V-axis Coarse Positions 0-10

These expanded views show how the gaps have, in general, been removed. However, these views also show that there are taps for which the distribution is not flat. In some cases, notably the V-axis projection from 25 - 35, the distribution peaks toward the center of each tap. This would be improved by adopting quadratic degap coefficients (see the corresponding projection image here). The projection for U-axis coarse positions 50 - 60 is more puzzling. The saw-tooth pattern along the distribution is almost certainly not due to variations in the illumination pattern and it is also difficult to understand why the detector efficiency would show such a pattern. Additional examination of the data reveal that the saw-tooth pattern is mainly produced by events with the highest pulse-heights. There is most likely some feature of the instrument electronics that is causing this systematic effect. A linear degap coefficient will not remove this systematic effect. A quadratic correction may be more successful. However, the corresponding quadratic projection still exhibits odd systematic behavior.

Expanded views of the projections

U-axisV-axis
0-10 0-10
10-20 10-20
20-30 20-30
30-40 30-40
40-50 40-50
50-60 50-60

Details of the quadratic degap coefficients can be found here.

Back to "Deriving HRC-I Degap for XRCF Settings (Flat Field Data)"

Back to "HRC Degapping Corrections"

Dr. Michael Juda
Harvard-Smithsonian Center for Astrophysics
60 Garden Street, Mail Stop 70
Cambridge, MA 02138, USA
Ph.: (617) 495-7062
Fax: (617) 495-7356
E-mail: mjuda@cfa.harvard.edu