The Low Energy Transmission Grating (LETG) is a large optical system that cannot be calibrated as a complete system effectively prior to delivery at the X-ray Calibration Facility. It can and will be characterized at the component level before delivery. The goal of these subassembly measurements is to specify the location, orientation, and period as well as the expected X-ray diffraction efficiency as a function of energy and diffraction order for each LETG facet.
The LETG is composed of 540 grating facets, held in groups of three within modules. The 180 modules are held in a Rowland torus configuration by the grating element support structure (GESS). Fabrication of the LETG instrument is a collaborative effort between the Space Research Organization Netherlands in Utrecht (SRON) and the Max Planck Institut für extraterrestrische Physik in Garching (MPE). MPE has the responsibility of characterizing individual grating facets and assembling them in threes into modules that will be mounted on the GESS at SRON. The characterization tests that will be performed by MPE are: grating facet inspection for defects, laser diffraction determination of grating facet period, near infrared transmission spectroscopy for determination of grating bar geometry, X-ray diffraction efficiency measurements on a small sample basis, and measurement of the alignment angle of each facet within the module. SRON has the responsibility of manufacturing and characterizing the GESS and for measuring the as-mounted alignments of the module/facet assemblies.
Grating facets are manufactured by Heidenhain GmBH and delivered in batches to MPE. A grating facet consists of gold grating ``foil'' bonded to a stainless steel cylinder. Approximately 1300 facets will be produced for the flight LETG, including spares. As the facets are received at MPE they undergo a visible inspection to detect any gross problems: large defects, wrinkles, etc.. Faults in the grating structure could lead to the destruction of large areas of a facet during the launch acoustic loads. Automated examination is accomplished using spatially filtered imaging of each facet in transmitted, polarized, near infrared illumination (Lochbihler, et al., 1996). Analysis of the resulting image returns a histogram of the sizes of the individual defects.
The grating facet period is determined by using the grating in
transmission to diffract light from a HeCd laser ( 
=441.6 nm).
Light from the laser is directed through a beam expander ( 
100)
and the expanded beam is limited by a 12 mm 5mm aperture
before the facet is illuminated.
A photodiode is mounted at the aperture plane as a reference for the
intensity of the illumination.
The grating is held in a mount which has two adjustments: one to
rotate the grating about its normal in order to adjust the plane of
diffraction and the second to rotate the grating about the normal to
the diffraction plane in order to obtain normal incidence illumination
of the facet.
The diffracted light is focused onto a slit 5 
m wide and 3 mm
high in front of a photodiode.
This lens, slit, and photodiode are mounted on an arm so that they can
move together as a unit.
The angular position of the arm is read using an encoder with a
precision of 
.
The arm is scanned across the diffraction peaks under computer control
and the ratio of the current in the detector photodiode to the current
in the monitor photodiode is obtained
for each point in the scan.
One pair of diffraction peak scans is plotted in
figure 6.
The grating period is determined from the means of both first order
spectra.
The resolving power of the facet is estimated by fitting a scalar
diffraction model to these first order diffraction patterns.
The real resolving power of the LETGS will not be measured until the XRCF
calibration
as the performance of the HRMA is a dominant contributor over most of
the X-ray range.
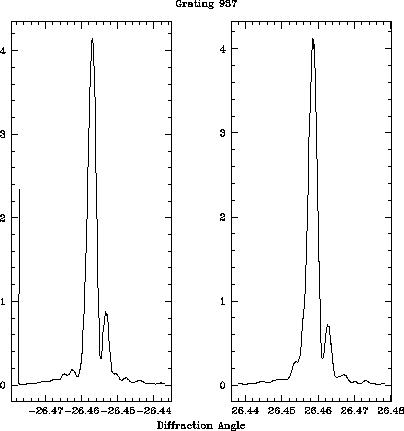
Figure 6: Example of angle scans of a grating facet from the laser
diffractometer.
The grating bar cross section profile determines the X-ray diffraction
efficiency of the grating facet.
Grating bar cross section profiles are approximated by trapezoids.
The grating bar profile is characterized by using the fact that the
gratings are good polarizers in the near infrared.
The theory behind this has been extensively
developed (Lochbihler and Depine 1993a, 1993b, and 1993c).
Characterization measurements are carried out in a commercially
available transmission spectrometer in which the transmission is
determined by comparing the signal for a light path through the sample
to the signal for a reference light path.
The spectrometer has been modified to include: a Glan prism,
apertures, and hardware to hold and position the facet.
The prism linearly polarizes the light with its electric field vector
perpendicular to the grating wire direction.
For each facet a transmission spectrum over the wavelength range
0.9-2.8 m is recorded.
The measurement takes 
5 min per facet as compared to half a day
per facet for X-ray diffraction measurements.
The three characteristic trapezoid dimensions, thickness, width, and
slope, are derived by using three characteristic numbers determined
from the NIR transmission spectrum: the wavelength of the transmission
peak, the amplitude of the peak, and the minimum amplitude for
wavelengths longward of the peak.
The wavelength of the peak is most strongly coupled to the thickness
of the bars, the minimum amplitude longward of the peak is most
strongly coupled to the width of the bars, and the amplitude of the
peak is most strongly coupled to the slope of the sides.
The relationships connecting the bar parameters to the spectral shape
parameters are based on the results of modeling of the expected
spectrum for a given input bar geometry.
Figure 7 is an example of one of the spectra.
X-ray diffraction efficiency measurements have been made for a few of the grating facets. This is partially done to verify the reliability of the method of deriving grating bar profiles from the polarized near infrared transmission spectra and partially to derive values for the complex refractive index at X-ray wavelengths for the gold used in fabricating the LETG facets. X-ray diffraction measurements were performed at the ZETA facility at MPE and at the BESSY synchrotron. At the ZETA facility diffraction efficiencies were measured for 9 energies in the interval 275-2000 eV. At BESSY, the diffraction efficiency was measured in fine steps over the range 100-1350 eV for several facets with different grating bar profiles. These data have been used to derive values for the complex index of refraction of the as-plated gold in the LETG facets.
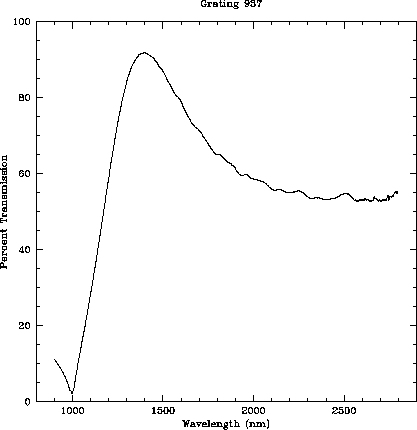
Figure 7: Example of NIR transmission spectrum of grating facet.
All the grating bars on the facets of the LETG should be aligned in
the same direction.
The LETG design leaves no alignment adjustment when mounting grating
modules on the GESS.
The alignment angle of the facets within a module are specified to MPE
by SRON based on the module's designated mounting location on the GESS
and measurements of the as-built GESS.
The gratings are aligned within the modules by taking advantage of their
polarization capabilities in the near infrared.
The alignment technique has been described in Anderson et
al. (1988) and Lochbihler et al. (1995).
A near infrared light source is directed through a Glan prism
polarizer and then through a photoelastic modulator (PEM) to generate
a polarization modulated beam of light.
The prism and PEM are mounted on a table that can be rotated with the
position angle readable to .
The polarized beam is directed through the grating facet and into a
photodiode.
A lock-in amplifier is used to detect the second harmonic of the
modulated polarization.
The signal is proportional to the sine of the angle between the
grating bars and the mean polarization axis.
The facet is rotated to null the second harmonic, aligning the facet
with the polarized beam.
The facet is then epoxied to the module.
Once the epoxy has cured the measurement is redone to determine the
alignment angles of the facets.
One complication that must be corrected for in this alignment process is the contribution of the support structure to the total polarization. There is roughly 1 arcsec of correction for every arcmin the fine support structure is away from perpendicular to the grating bars. The misalignment of the grating and support structure wire directions are determined by grabbing video frames of images of the grating bars and fine support structure bars taken under the microscope. Two different images are required because the widely different periods of the two structures require different magnification. Fourier analysis techniques are then be used to determine the position angle of the wires within the images.
The GESS holds each grating module to position the centers of the central grating facet on the Rowland torus with the facet normal pointing to the on-axis focus. The mounting plane for a given module is defined by six values: three that determine its location in space and three that determine its orientation. The three location quantities are determined by mechanical measurement of reference points on the mounting surfaces on a measuring table. The rotation angle about the optic axis of the module mounting surface must be known prior to alignment of the facets within the module so that the grating bars will be correctly aligned. This angle is measured by mounting a dummy module with a flat mirror to the GESS and using an autocollimator. The flat mirror is oriented to reflect light in the plane perpendicular to the optical axis of the LETG. The deviation of the rotation angle of the module about the optic axis from its design value is measured for each of the GESS/modules interfaces. These deviations are used to calculate the required facet alignment angles within the modules specified to MPE.
Once the grating modules are mounted, the facet normal directions are measured using reflection measurements in ``autocollimation'' from the facets. Additionally, the as-mounted grating bar alignments for individual facets are measured using the diffraction of visible light. Laser light is directed through each facet toward the system focus and the location of the first order diffracted beam is measured.
The subassembly calibration program is designed to obtain data from the LETG components that will enable us to develop a model for the LETG as an assembled system. Our model for the LETG will be used to predict the performance we should see at the XRCF. Based on the results of XRCF measurements we may need to modify our LETG model in preparation for making predictions of on-orbit performance.
For more information on the grating facet characterization visit the LETG HomePage at MPE.
E. H. Anderson, A. M. Levine, and M. L. Schattenburg, ``Transmission X-ray diffraction grating alignment using a photoelastic modulator'', Appl. Opt., 27, 3522-3525 (1988).
H. Lochbihler, C. Rotsch und P. Predehl, ``Recognition of Damage in Polarizing Transmission-Grating Facets'', Appl. Opt. 35, 826-831 (1996).
H. Lochbihler und R. A. Depine, ``Highly conducting wire gratings in the resonance region'', Appl. Opt. 32, 3459-3465 (1993a).
H. Lochbihler und R. A. Depine, ``Characterization of highly conducting wire gratings using an electromagnetic theory of diffraction'', Opt. Commun. 100, 231-239 (1993b).
H. Lochbihler und R. A. Depine, ``Diffraction from Highly Conducting Wire Gratings of Arbitrary Cross Section'', Journ. Mod. Opt. 40, 1273-1298 (1993c).
H. Lochbihler, E. Polnau und P. Predehl, ``Polarimetry of Transmission Gratings'', Appl. Opt. 34, 5725-5731 (1995).
Michael Juda