Sherpa Optimization Methods
-
Available Optimization Methods: each optimization method described in detail.
Introduction
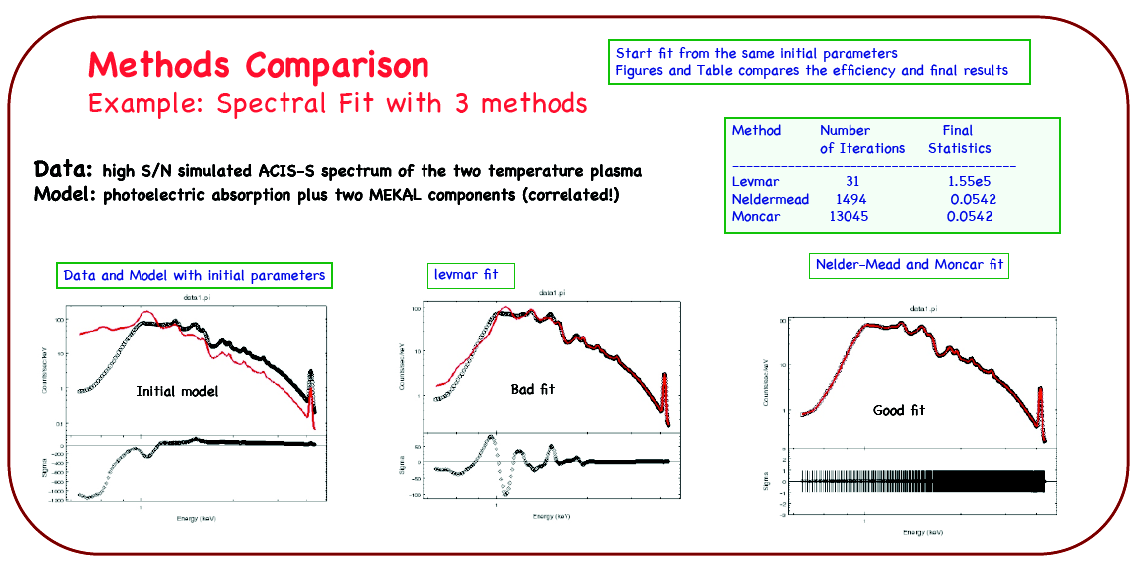
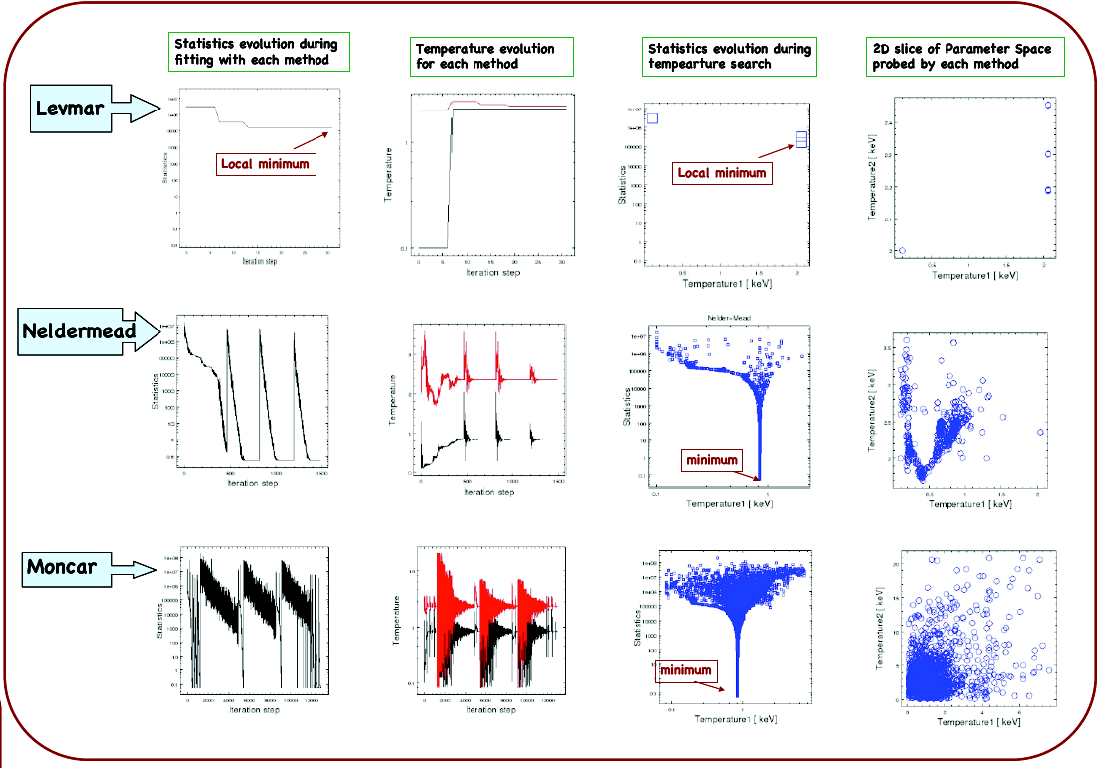
The "forward-fitting" algorithm employed by the Sherpa software package is a standard technique used to model X-ray data. A statistic, usually an assumed weighted chi2 or Poisson likelihood (e.g. Cash), is minimized in the fitting process to obtain a set of the best model parameters. Astronomical models often have complex forms with many parameters that can be correlated (e.g. an absorbed power-law); minimization is not trivial in such a setting, as the statistical parameter space becomes multimodal, and finding the global minimum is difficult. Therefore we have developed several optimization algorithms in Sherpa which target a wide range of minimization problems. Two local minimization methods were built: the Levenberg-Marquardt algorithm was obtained from the MINPACK subroutine LMDIF and modified to achieve the required robustness; and the Nelder-Mead simplex method has been implemented in-house based on variations of the algorithm described in the literature. A global search Monte-Carlo method has been implemented following a differential evolution algorithm presented by Storn and Price (1997). Below we present the methods in Sherpa and discuss their performance in complex X-ray spectral model application to Chandra high S/N data.
Optimization Methods
- Optimization - finding a parameter value for which a statistics function has a minimum (or a maximum).
-
Requirements for the optimization methods in Sherpa:
- Applicable to a variety of problems in modeling X-ray data, e.g., low- and high-counts Poisson data.
- Robust when applied to complex models.
Local Methods:
- Calculates derivatives of a statistics function over the parameter space of the function .
- Appropriate for chi2 statistics.
- Convergence when the difference in the statistics in the iterative steps is smaller than the required tolerance.
- Fast, but very dependent on initial conditions; known to fail in complex cases with poor initial parameter values.
- Sherpa's levmar method is based on the LMDIF subroutine (from the MINPACK library of FORTRAN subroutines).
-
Starts from an initial set of parameters and then
improves the parameters in a continuous fashion:
- Non-derivative method, no gradient information.
- Convergence when the statistics at the vertices are small or the simplex is small.
- Sherpa includes simplex as an implementation of the Nelder-Mead algorithm (Nelder & Mead, 1965, Computer Journal, vol 7, 308-313).
Global Methods:
- Random selection of parameters from the entire permitted parameter space.
- Includes conditions for a "smart" selection of parameters to improve efficiency of the search.
- Sherpa's moncar method is an implementation of the Differential Evolution algorithm based on Storn and Price (J. Global Optimization 11, 341-359, 1997; http://www.icsi.berkeley.edu/~storn/code.html).
Evaluates the fit statistic for each point in a user-specified parameter space grid, and returns the parameter values associated with the grid point with the lowest value of the fit statistic (the best match).
Summary
- levmar is fast, very sensitive to initial parameters, and performs well for simple models, e.g. power-law or single-temperature models, but fails to converge with complex models.
- neldermead and moncar are both very robust and converge to the global minimum in complex model cases.
- neldermead is more efficient than moncar, but moncar probes a larger part of the parameter space.
- moncar or neldermead should be used when fitting complex models with correlated parameters.
Global Methods: Monte-Carlo